A simple example of a reversible polytropic process is the polytropic change of an ideal gas. This process is defined by the equation pVn=const, where p is the pressure of the gas, V is the volume of the gas, and n = (C— CP)/(C— Cv) is the polytropic exponent (Cp and Cv are thespecific heats of the gas at constant pressure and constant volume, respectively). By using the equation of state for an ideal gas, the equationof a polytropic curve can be written in a different form: pTn/(1-n)= const or VT1(1-n) = const, here T is the absolute temperature. Special casesof the equation of a polytropic process for an ideal gas are the equations for an isentropic curve, where C = 0 and n = Cp/cv (this ratio ofspecific heats is designated γ); an isobar, where C— Cp and n = 0; an isochor, where C= Cv and n = ∞; and an isotherm, where C= ∞ and n =1. The work A done by an ideal gas against the ambient pressure is determined from the formula
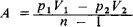
where the subscripts 1 and 2 refer to the initial and final states of the gas.
Engineering thermodynamics makes extensive use of
the concept of
polytropic processes in
investigating the operating cycles of
heatengines."Pantropic" redirects here. For the term used in distributions, see pantropical.

where
p is the pressure,
v is specific volume,
n, the
polytropic index, is any
real number, and
C is a constant. The polytropic process equation is particularly useful for characterizing expansion and compression processes which include heat transfer. This equation can accurately characterize a very wide range of
thermodynamic processes, that range from n=0 to n=

which covers, n=0 (
isobaric), n=1 (
isothermal), n=γ (
isentropic), n=

(
isochoric) processes and all values of n in between. Hence the equation is polytropic in the sense that it describes many lines or many processes. In addition to the behavior of gases, it can in some cases represent some
liquids and
solids. The one restriction is that the process should display an energy transfer ratio of K=δQ/δW=constant during that process. If it deviates from that restriction it suggests the exponent is not a constant. For a particular exponent, other points along the curve can be calculated:
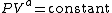
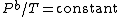


 which covers, n=0 (isobaric), n=1 (isothermal), n=γ (isentropic), n=
which covers, n=0 (isobaric), n=1 (isothermal), n=γ (isentropic), n= (isochoric) processes and all values of n in between. Hence the equation is polytropic in the sense that it describes many lines or many processes. In addition to the behavior of gases, it can in some cases represent some liquids and solids. The one restriction is that the process should display an energy transfer ratio of K=δQ/δW=constant during that process. If it deviates from that restriction it suggests the exponent is not a constant. For a particular exponent, other points along the curve can be calculated:
(isochoric) processes and all values of n in between. Hence the equation is polytropic in the sense that it describes many lines or many processes. In addition to the behavior of gases, it can in some cases represent some liquids and solids. The one restriction is that the process should display an energy transfer ratio of K=δQ/δW=constant during that process. If it deviates from that restriction it suggests the exponent is not a constant. For a particular exponent, other points along the curve can be calculated:
Tidak ada komentar:
Posting Komentar