Senin, 16 Maret 2015



Quasi-static processes


Consider the special case of an interaction of the system $A$ with its surroundings which is carried out so slowly that $A$ remains arbitrarily close to equilibrium at all times. Such a process is said to be quasi-static for the system $A$. In practice, a quasi-static process must be carried out on a time-scale which is much longer than the relaxation time of the system. Recall that the relaxation time is the typical time-scale for the system to return to equilibrium after being suddenly disturbed (see Sect. 3.5).A finite quasi-static change can be built up out of many infinitesimal changes. The infinitesimal heat $\,{\mathchar'26\mskip-12mud}Q$ absorbed by the system when infinitesimal work $\,{\mathchar'26\mskip-12mud}W$ is done on its environment and its average energy changes by $d \bar{E}$ is given by 

\begin{displaymath} {\mathchar'26\mskip-12mud}Q \equiv d\bar{E} + {\mathchar'26\mskip-12mud}W. \end{displaymath}(124)


The special symbols $\,{\mathchar'26\mskip-12mud}W$ and $\,{\mathchar'26\mskip-12mud}Q$ are introduced to emphasize that the work done and heat absorbed are infinitesimal quantities which do not correspond to the difference between two works or two heats. Instead, the work done and heat absorbed depend on the interaction process itself. Thus, it makes no sense to talk about the work in the system before and after the process, or the difference between these.If the external parameters of the system have the values $x_1$, $\cdots, x_n$ then the energy of the system in a definite microstate $r$ can be written 

\begin{displaymath} E_r = E_r(x_1,\cdots, x_n). \end{displaymath}(125)


Hence, if the external parameters are changed by infinitesimal amounts, so that $x_\alpha \rightarrow x_\alpha + dx_\alpha$ for $\alpha$ in the range 1 to $n$, then the corresponding change in the energy of the microstate is 
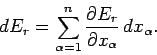\begin{displaymath} d E_r = \sum_{\alpha =1}^n \frac{\partial E_r}{\partial x_\alpha}\,dx_\alpha. \end{displaymath}(126)


The work $\,{\mathchar'26\mskip-12mud}W$ done by the system when it remains in this particular state $r$ is 
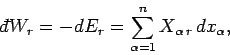\begin{displaymath} {\mathchar'26\mskip-12mud}W_r = - d E_r = \sum_{\alpha=1}^n X_{\alpha\,r}\,dx_\alpha, \end{displaymath}(127)


where 
\begin{displaymath} X_{\alpha\,r} \equiv -\frac{\partial E_r}{\partial x_\alpha} \end{displaymath}(128)


is termed the generalized force (conjugate to the external parameter $x_\alpha$) in the state $r$. Note that if $x_\alpha$ is a displacement then $X_{\alpha\,r}$ is an ordinary force.Consider now an ensemble of systems. Provided that the external parameters of the system are changed quasi-statically, the generalized forces $X_{\alpha\,r}$ have well defined mean values which are calculable from the distribution of systems in the ensemble characteristic of the instantaneous macrostate. The macroscopic work $\,{\mathchar'26\mskip-12mud}W$ resulting from an infinitesimal quasi-static change of the external parameters is obtained by calculating the decrease in the mean energy resulting from the parameter change. Thus, 

\begin{displaymath} {\mathchar'26\mskip-12mud}W = \sum_{\alpha =1}^n \bar{X}_\alpha\, dx_\alpha, \end{displaymath}(129)


where 
\begin{displaymath} \bar{X}_\alpha \equiv -\overline{ \frac{\partial E_r}{\partial x_\alpha}} \end{displaymath}(130)


is the mean generalized force conjugate to $x_\alpha$. The mean value is calculated from the equilibrium distribution of systems in the ensemble corresponding to the external parameter values $x_\alpha$. The macroscopic work $W$ resulting from a finite quasi-static change of external parameters can be obtained by integrating Eq. (129).The most well-known example of quasi-static work in thermodynamics is that done by pressure when the volume changes. For simplicity, suppose that the volume $V$ is the only external parameter of any consequence. The work done in changing the volume from $V$ to $V + dV$ is simply the product of the force and the displacement (along the line of action of the force). By definition, the mean equilibrium pressure $\bar{p}$ of a given macrostate is equal to the normal force per unit area acting on any surface element. Thus, the normal force acting on a surface element $d{\bf S}_i$ is $\bar{p}\,\,d{\bf S}_i$. Suppose that the surface element is subject to a displacement $d{\bf x}_i$. The work done by the element is $\bar{p}\,\,d{\bf S}_i \!\cdot\! d{\bf x}_i$. The total work done by the system is obtained by summing over all of the surface elements. Thus, 

\begin{displaymath} {\mathchar'26\mskip-12mud}W = \bar{p}\, \,dV, \end{displaymath}(131)


where 
\begin{displaymath} dV = \sum_i d{\bf S}_i\!\cdot\! d{\bf x}_i \end{displaymath}(132)


is the infinitesimal volume change due to the displacement of the surface. It follows from (130) that 
\begin{displaymath} \bar{p} = - \frac{ \partial\bar{E} }{\partial V}, \end{displaymath}(133)


so the mean pressure is the generalized force conjugate to the volume $V$.Suppose that a quasi-static process is carried out in which the volume is changed from $V_i$ to $V_f$. In general, the mean pressure is a function of the volume, so $\bar{p} = \bar{p}(V)$. It follows that the macroscopic work done by the system is given by 

\begin{displaymath} W_{if} = \int_{V_i}^{V_f} {\mathchar'26\mskip-12mud}W = \int_{V_i}^{V_f} \bar{p}(V)\, dV. \end{displaymath}(134)


This quantity is just the ``area under the curve'' in a plot of $\bar{p}(V)$ versus $V$.

It is important to distinguish between reversible and quasistatic processes. Reversible processes are always quasistatic, but the converse is not always true. For example, an infinitesimal compression of a gas in a cylinder where there exists friction between the piston and the cylinder is a quasistatic process, but not reversible process. Although the system has been driven from its equilibrium state by only an infinitesimal amount, heat has been irreversibly lost due to friction, and cannot be recovered by simply moving the piston infinitesimally in the opposite direction."
See this video link for further details.
  • 2
    •  
  •  Link
    up vote1down votefavorite
    Let us start from definitions, as they are given in many sources.
    A quasistatic process is an idealized processes that happen out so slowly that a system go through a sequence of states arbitrarily close to equilibrium.
    An isobaric process is a process, in which the pressure remains constant.
    An isochoric process is a process, in which the volume remains constant.
    An isothermal process is a process, in which the temperature remains constant.
    Now, I could imagine how an isochoric process could not be quasistatic, but what about isobaric and isothermal processes?
    For instance, for the following specific example (from Count Iblis answer):
    Suppose we put a mixture of hydrogen gas and oxygen gas in a conducting cylinder that is kept at constant volume and in thermal contact with a heat bath. There is also a device in the cylinder that will produce a spark, igniting the gas.
    I indeed object (as Count Iblis expected) that the process of ignition is isothermal: when we ignite the mixture chemical reaction takes place, the huge amount of heat is liberated, and besides, a complicated movement of the gas mixture occurs. Thus, it does not make a lot of sense to speak about keeping the temperature of the system constant, since the temperature is different even in different regions of the system. This should not surprise us, since right after the ignition and for some time then the system is clearly not in equilibrium, and thus, the notion of the temperature of the system is not even defined.
    So, if we adopt this definition then, an isothermal process imply a quasistatic one, since it does not make sense to talk about constant temperature in a process that is not quasistatic, since temperature is not even well-defined in intermediate non-equilibrium states of such process.
    In other words, the presence of the heat bath is not enough for the process described above to be isothermal: the process should also be performed slowly enough so that all heat liberated can be almostinstantaneously transferred to the surroundings. Only in such a case the temperature of the system is indeed constant during a process. Clearly, the system should be in thermal equilibrium with its surrounding all the way, and thus, I think that for the process to be isothermal, it should be quasistatic.
    Am I right?
    P.S. Oh, how I feel like I see where I went wrong. An isothermal process indeed must happen at such a slow rate that the thermal equilibrium is maintained, however, thermal equilibrium is not the whole story. As we know systems in thermodynamic equilibrium are always in thermal equilibrium, but the converse is not always true. So, since only thermal equilibrium is required for an isothermal process, it is not necessarily quasistatic. A quasistatic process is always arbitrarily close to thermodynamic equilibrium, while isothermal is only in thermal equilibrium.
    Diposting oleh di

    Tidak ada komentar:

    Posting Komentar

    Langganan: Posting Komentar (Atom)